
No artigo anterior, falamos sobre o conceito de equilíbrio na termodinâmica, desenvolvemos a equação fundamental da termodinâmica e introduzimos rapidamente o potencial químico. Hoje, vou aprofundar com vocês:
- o que é o potencial químico
- como surge a equação de equilíbrio de fases, além de discutir o conceito de
- conceito de fugacidade e de coeficiente de fugacidade
A principal referência que utilizei para escrever este artigo foi o Introdução a Termodinâmica da Engenharia Química, um texto de cabeceira que todo engenheiro químico deve ter. Se quiser adquirir o livro, clique no link acima.
Tabela de Conteúdo
Equilíbrio Termodinâmico
A segunda lei da termodinâmica nos diz que a entropia total do universo sempre aumenta; quando não, ao menos não varia.
Como o universo é a soma do sistema que estamos estudando com suas vizinhanças, então isso quer dizer que, para a entropia de um sistema diminuir, a entropia das vizinhanças deve aumentar. Isto é chamado de balanço de entropia.
Do balanço de entropia, temos:
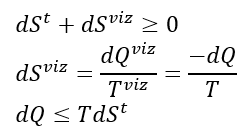
Mas, da primeira lei:
Ou:
De modo que:
Ou:
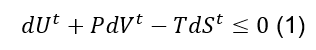
A equação (1), Apesar de ter validade geral para sistemas fechados em processos reversíveis e irreversíveis, ela é de aplicação limitada. Usando restrições comuns, como T e P constantes, podemos usar a seguinte notação:
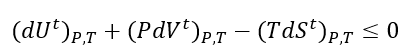
Se T e P são constantes, então não faz diferença se reescrevermos como
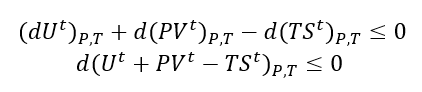
Entretanto, lembrando a definição de Energia de Gibbs e de Entalpia:
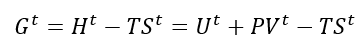
Teremos por fim:
A equação (2) nos diz que toda transformação irreversível que ocorrem a T e P constantes caminham na direção da diminuição da Energia de Gibbs. Além disso, nos diz também que, no equilíbrio:
A equação (3) é extremamente útil para problemas de equilíbrio químico e equilíbrio de fases, que é a nossa tarefa.
Potencial Químico
A equação fundamental da termodinâmica, como foi escrita no artigo anterior, possui outras formas equivalentes, também chamadas de equações fundamentais. Uma delas é
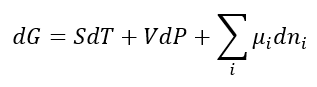
Onde mi i é o potencial químico da substância i, e dn i é uma variação infinitesimal da quantidade de matéria de i. Esta equação nos informa que é possível variar o conteúdo energético do sistema mediante uma variação na temperatura, na pressão ou na quantidade de massa que entra ou escapa do sistema.
Como as funções de estado (como é o caso da energia de Gibbs) são diferenciais exatas, uma rápida inspeção da equação fundamental nos permite concluir que:
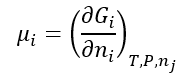
Ou seja, o potencial químico é uma propriedade parcial molar referente a substância i, mais especificamente, uma energia de Gibbs parcial molar da substância i. Repare que isto não significa que o potencial químico é uma constante, justamente porque ela depende do valor da coordenada .
Equilíbrio de Fases
Imagine o seguinte sistema bifásico em equilíbrio, composto por água e um orgânico parcialmente solúvel em água (i=2):

Nesta situação, cada fase possui seu conteúdo energético, e podemos dizer que:
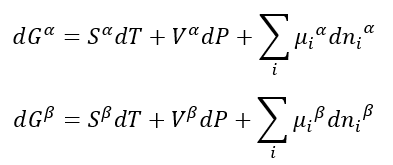
Onde alfa e beta indicam as fases. Como T e P são constantes, e o conteúdo energético total Gt é a soma do conteúdo energético de cada uma das fases, então podemos escrever:
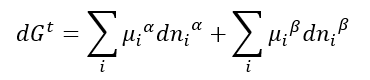
Mas, como já vimos, a condição de equilíbrio termodinâmico é mandatória:
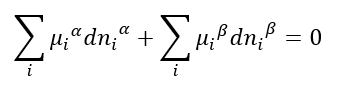
Por outro lado, o equilíbrio de fases é dinâmico: a todo momento moléculas de i escapam de uma fase e vão para outra, e vice versa. Portanto, um balanço de massa simples nos permite dizer que:
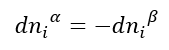
De modo que a condição de equilíbrio se torna:
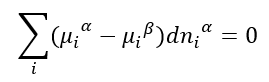
Como nada nos diz que dn i seja zero, então, chegamos à conclusão de que
A equação (4) é uma igualdade que descreve o equilíbrio de fases em termos da igualdade do potencial químico de cada substância em cada fase. Se por um acaso houver uma diferença no potencial químico dessa substância, há o deslocamento (transporte) das moléculas visando a minimização da energia livre de Gibbs (lembre-se: o potencial químico não é senão a energia de Gibbs). Este é o princípio da difusão e da transferência de massa.
Fugacidade
A equação (4) tem um inconveniente matemático: o potencial químico pode assumir valores infinitamente negativos. Vejamos o porquê.
Retomando a equação fundamental da termodinâmica (para a energia de Gibbs), e assumindo um sistema fechado de 1 mol de um gás i puro e um processo isotérmico, temos:
Usando a lei de gases ideais,

Obtemos:
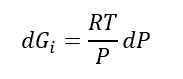
Logo,
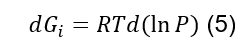
Ou
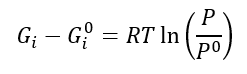
Esta igualdade só tem validade para gases ideais. Para torná-la aplicável a gases reais, utilizemos uma nova coordenada que corrija essa não-idealidade, e chamemo-la de fugacidade.
Esta nossa nova coordenada, que possui unidade de pressão, deve, entretanto, se aproximar do próprio valor de pressão quando nosso gás real se aproximar do comportamento de gás ideal.
Isto só acontece quando a pressão absoluta tende a zero. Escrevendo em termos matemáticos:
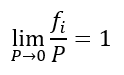
Esta é uma restrição que define o que é fugacidade e que será de grande utilidade.
Olhando agora sob a perspectiva de uma mistura de gases, nossa pressão P se torna a pressão parcial da substância i, e nossa fugacidade da substância i pura se torna a fugacidade da substância i em solução:
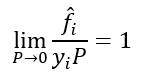
Como estamos tratando de uma mistura de gases agora, então dG i é substituído por d mi i:
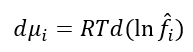
Ou:
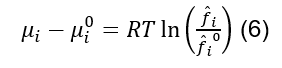
Olhando de outra maneira, podemos afirmar que, para mistura de gases ideais, a fugacidade de um componente i é
E, para um estado arbitrário de referência:
Assume-se que esse estado de referência já está próximo da idealidade (1 bar de pressão).
Além disso, podemos chamar o “desvio percentual” da idealidade (razão f/P) de coeficiente de fugacidade:
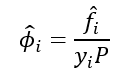
Se aproximarmos P→P°, como P° é suficientemente próximo da idealidade, então a seguinte cadeia lógica é válida:
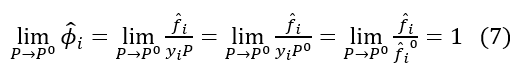
Vamos agora recapitular: a equação (5) nos diz como a energia de Gibbs de um mol de um gás ideal varia conforme variamos a pressão a que este gás está submetido.
Entretanto, além da limitação de aplicação a apenas gases ideais, um problema mais grave acontece: se diminuirmos demais a pressão, tende a um número infinitamente negativo.
Por outro lado, se utilizarmos uma coordenada equivalente a pressão como a fugacidade, e definirmos uma referência para o que se considera idealidade, então, sempre que reduzirmos a pressão, a expressão (6) será um valor finito, devido à nossa descoberta (7).
Esta é a grande vantagem do uso da fugacidade: ela nos permite: 1) Definir uma função desvio (o coeficiente de fugacidade); 2) Definir uma referência arbitrária de modo que 3) O inconveniente matemático decorrente de uma baixa pressão não mais exista.
Equilíbrio de fases em termos de fugacidade
Se (6) é válido, então podemos reescrever o equilíbrio de fases como sendo:
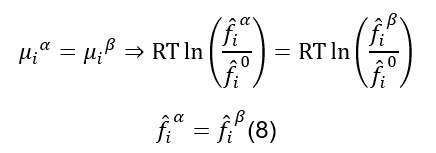
A equação (8) é muito mais conveniente que a equação (4) para
cálculos de equilíbrio de fases, e é a equação básica para cálculos de Equilíbrio Líquido-Líquido, Líquido-Vapor, Sólido-Líquido, etc.
Conclusão
Continuamos nossa série de artigos sobre equilíbrio de fases, tema tão fundamental para o engenheiro químico, e tão pouco compreendido. Se quiser uma explicação mais detalhada, recomendo fortemente que adquira o livro dos senhores Smith, Van Ness, Abbott e Swilhart.
No próximo artigo, apresentarei alguns modelos termodinâmicos e quais deles você deve escolher para resolver os diversos problemas de equilíbrio de fases. Até a próxima!